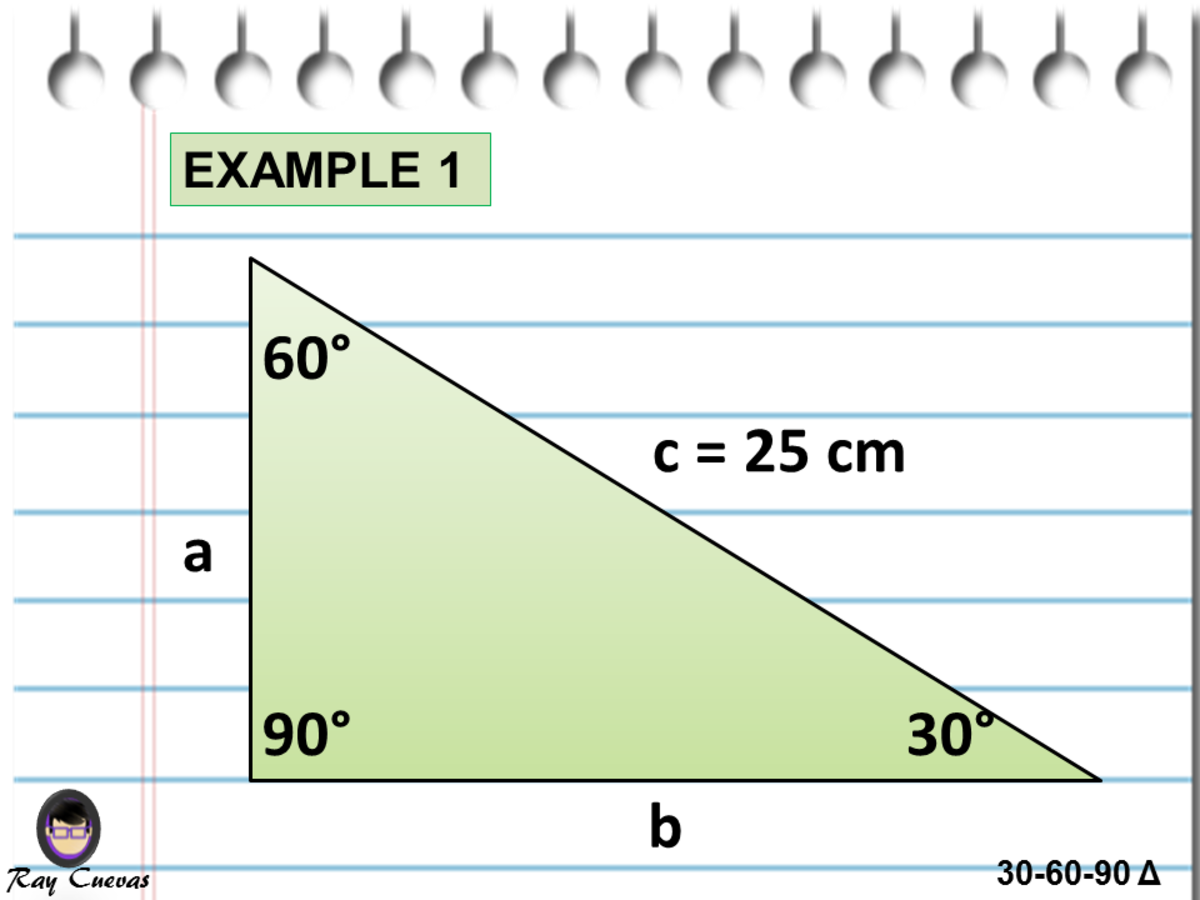
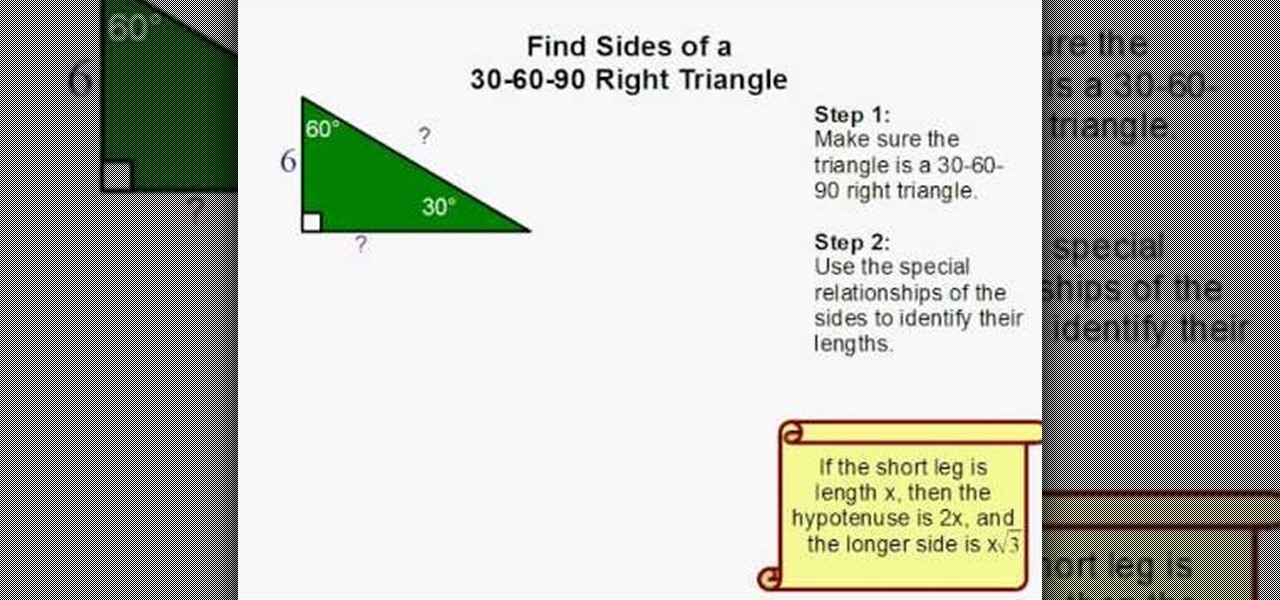
Use the properties of special right triangles described on this page) Show Answer The 30$$^{\circ}$$ and 60$$^{\circ}$$ angles give this one away x = 6A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are also always inTriangles are classified as "special right triangles" They are special because of special relationships among the triangle legs that allow one to easily arrive at the length of the sides with exact answers instead of decimal approximations when using trig functions

Right Triangles 30 60 90 Special Right Triangles Notes And Practice
Right triangle formulas 30 60 90
Right triangle formulas 30 60 90- A right triangle is a special type of right triangle 30 60 90 triangle's three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1√ (3/2) This means that the hypotenuse is twice as long as the shorter leg and the longer leg is the square root of tan (60) = √3/1 = 173 The right triangle is special because it is the only right triangle whose angles are a progression of integer multiples of a single angle If angle A is 30 degrees, the angle B = 2A (60 degrees) and angle C = 3A (90 degrees)



The Easy Guide To The 30 60 90 Triangle
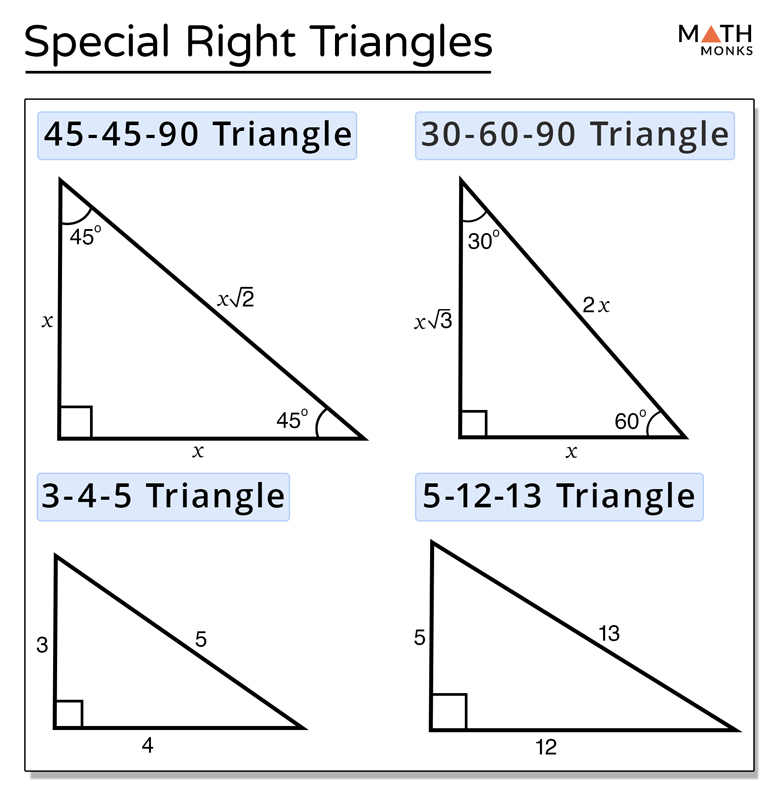
This method can be used to remember the triangle ruleThe ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x x Hypotenuse (opposite the 90 90 degree angle) = 2x 2 x Long side (opposite the 60 60 degree angle) = x√3 x 3Right Triangles Hypotenuse equals twice the smallest leg, while the larger leg is sqrt (3) times the smallest % Progress MEMORY METER This indicates how strong in your memory this concept is Practice Preview Assign Practice
The perimeter of a 30 60 90 triangle with the smallest side equal to a is the sum of all three sides The other two sides are a√3 and 2a The perimeter of the triangle is aa√32a = 3aa√3 = a√3 (1√3) Are There Any Tips for Remembering the Triangle Rules?Special Right Triangles A special right triangle is one which has sides or angles for which simple formulas exist making calculations easy Of all these special right triangles, the two encountered most often are the 30 60 90 and the 45 45 90 triangles For example, a speed square used by carpenters is a 45 45 90 triangleAnswer (1 of 3) This question definitely needs to be edited first I guess the question is Q What is the formula to find the hypotenuse in a 30 60 90 triangle If the question is as above FORMULA HYPOTENUSE = √{ s² (√3 s)²}, where s is a side length of the right triangle And obviou
30 60 90 Triangle Theorem Ratio And Formula Video Triangles On Sat Math Geometry Strategies And Practice How To Find The Sides Of A 30 60 90 Right Triangle Math Understanding 30 60 90 Triangles High School Math 30 60 90 Triangles Kates Math LessonsExample We multiply the length of the leg which is 7 inches by √2 to get the length of the hypotenuse $$7\cdot \sqrt{2}\approx 99$$ In a 30°60° right triangle we can find the length of the leg that is opposite the 30° angle by using this formula 60° x = 223, y = 22 12) u293 v 30° u = 58, v = 29 13) a36 b 60° a = 243, b = 123 14) x y 43 30° x = , y = 12 15) xy 45 60° x = 90, y = 453 16) x 323 y 30° x = 64, y = 32 17) 40 x y 30° x = 3, y = 18) x 333 2 y 30° x = 33, y = 33 2



File 30 60 90 Triangle 2 Svg Wikimedia Commons



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
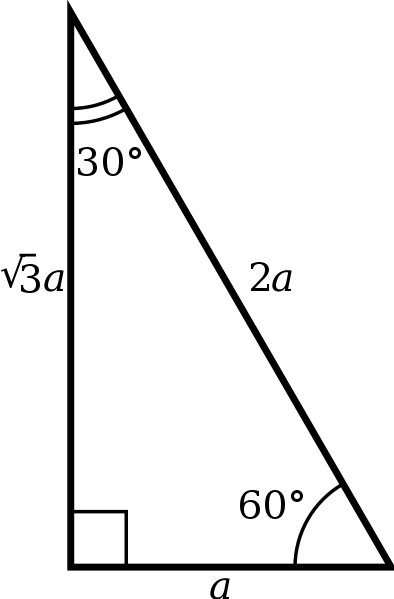
30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 b = c√3/2 Or simply type your given values and the 30 60 90 triangle calculator will do the rest! The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the30 60 90 triangle rules and properties The most important rule to remember is that this special right triangle has one right angle and its sides are in an easytoremember consistent relationship with one another the ratio is a a√3 2a Worksheet 45 ¡45 ¡90 triangleand30 ¡60 ¡90 triangle 1For the 45 ¡45 ¡90 triangle, (the isosceles right triangle), there are two legs of length a and the



1



The Easy Guide To The 30 60 90 Triangle
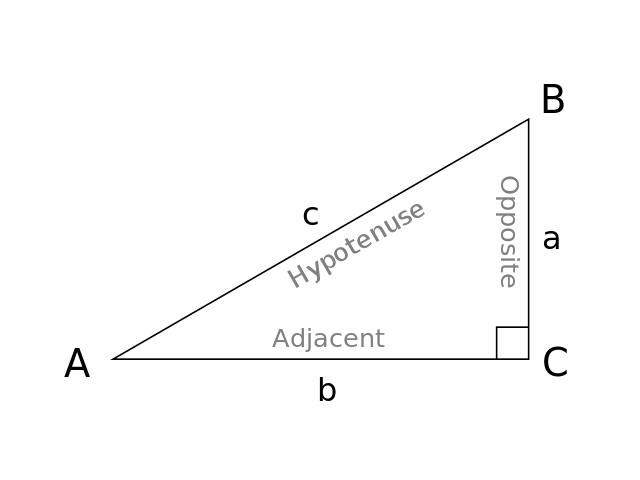
Using the pythagorean theorem – As a right angle triangle, the length of the sides of a 45 45 90 triangle can easily beFor any problem involving a 30°60°90° triangle, the student should not use a table The student should sketch the triangle and place the ratio numbers Since the cosine is the ratio of the adjacent side to the hypotenuse, you can see that cos 60° = ½ Example 2 Evaluate sin 30° Answer sin 30° = ½ You can see that directly in the figure aboveY√3 = Long side (opposite the 60° angle) These three special rules can be considered the triangle theorem and are unique to these special right triangles The hypotenuse (the triangle's longest side) is always twice the length of the short leg The length of the longer leg is the short leg's length times √3




Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Teaching Math




30 60 90 Triangles Hd Youtube
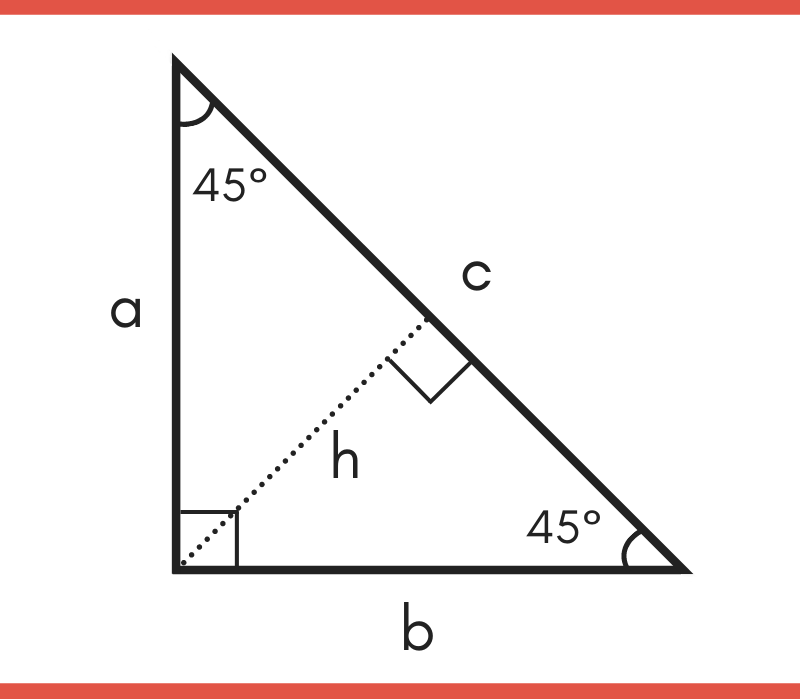
Special Right Triangles inA right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, andA 30̊ 60̊ 90̊ right triangle orThe 45°45°90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°45°90°, follow a ratio of 11√ 2 Like the 30°60°90° triangle, knowing one side length allows you to determine the lengths of the other sides Side opposite the 90° angle 2x All degree triangles have sides with the same basic ratio Two of the most common right triangles are and degree triangles If you look at the 30–60–90degree triangle in radians, it translates to the following In any triangle, you see the following




Learn About The 30 60 90 Triangle Caddell Prep Online




Special Right Triangles 45 45 30 60 90 Notes Sheet Graphic Organizers
Since this is a right triangle, we know that the sides exist in the proportion 1 √3 3 2 The shortest side, 1, is opposite the 30 degree angle Since side X is opposite the 60 degree angle, we know that it is equal to 1∗ √3 1 ∗ 3, or about 173Special Triangles Isosceles and Calculator This calculator performs either of 2 items 1) If you are given a right triangle, the calculator will determine the missing 2 sides Enter the side that is known After this, press Solve Triangle 2) In addition, the calculator will allow you to same as Step 1 with a right triangleIn any triangle, you see the following The shortest leg is across from the 30degree angle, the length of the hypotenuse is always double the length of the shortest leg, you can find the long leg by multiplying the short leg by the square root of 3 Are all isosceles triangles 30 60 90?




Right Triangles 30 60 90 Special Right Triangles Notes And Practice




30 60 90 Triangle Calculator Formula Rules
The main rule of triangles is that it has one right angle and while the other two angles each measure 45° 45 ° The lengths of the sides adjacent to the right triangle, the shorter sides have an equal length Another rule is that the two sides of the triangle or legs of the triangle that form the right angle are congruent in length What is the triangle formula?As one angle is 90, so this triangle is always a right triangle As explained above that it is a special triangle so it has special values of lengths and angles The basic triangle sides ratio is The side opposite the 30° angle x The side opposite



Special Right Triangles Definition Formula Examples




30 60 90 Right Triangles Solutions Examples Videos
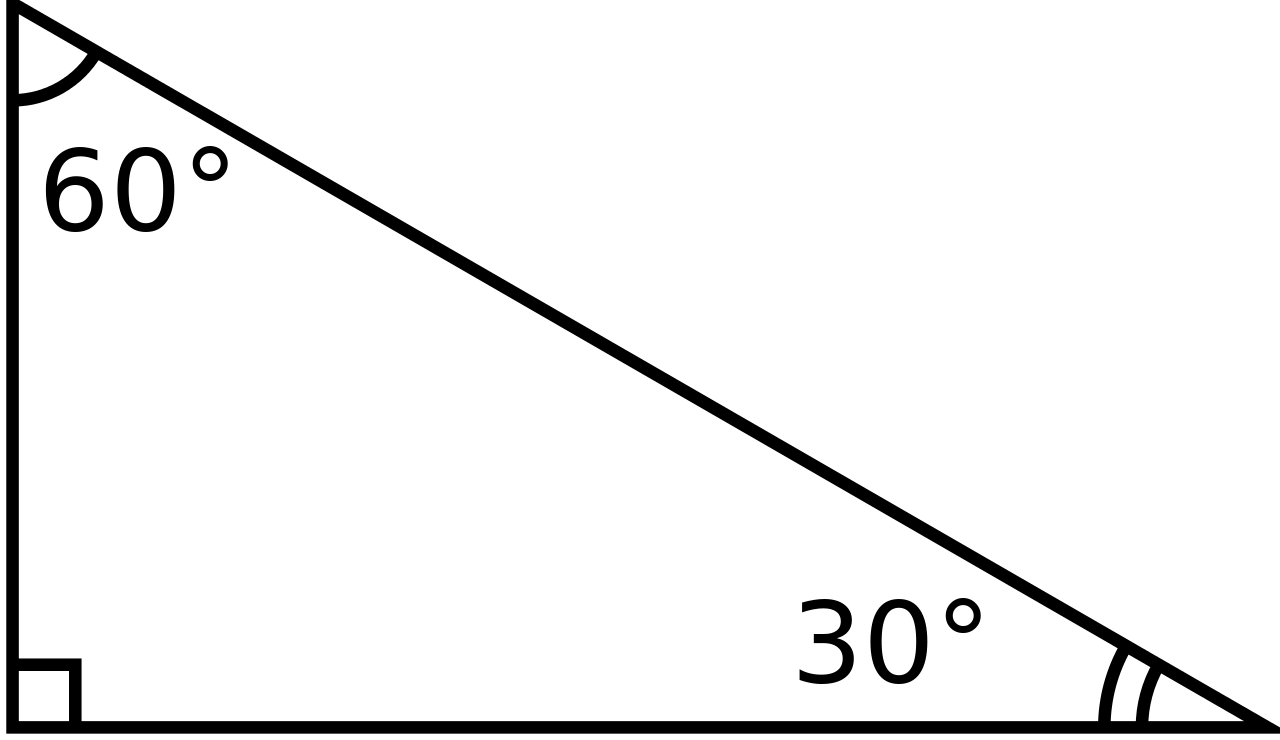
Triangles A triangle is a right triangle whose internal angles are 30, 60 and 90 degrees The three sides of a triangle have the following characteristics All three sides have different lengths The shorter leg, b, is half the length of the hypotenuse, c That is, b=c/2A triangle is a special right triangle whose angles are 30º, 60º, and 90º The triangle is special because its side lengths are always in the ratio of 1 √32 What is the formula for a 45 45 90 Triangle? A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another




Special Right Triangles Part 1 45 45 90 And 30 60 90 Youtube




30 60 90 Triangles




Right Triangles Interactive Notebook Pages Mrs E Teaches Math




30 60 90 Triangle Calculator Formula Rules



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



30 60 90 Triangle Formulas Rules And Sides Science Trends




30 60 90 Right Triangle Side Ratios Expii



30 60 90 Triangle Formulas Rules And Sides Science Trends




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



1




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet




The 30 60 90 Triangle Topics In Trigonometry




30 60 90 Triangle Theorem Ratio Formula Video



45 45 90 Special Right Triangle Calculator Inch Calculator




30 60 90 Triangle Theorem Ratio Formula Video



How To Find The Sides Of A 30 60 90 Right Triangle Math Wonderhowto
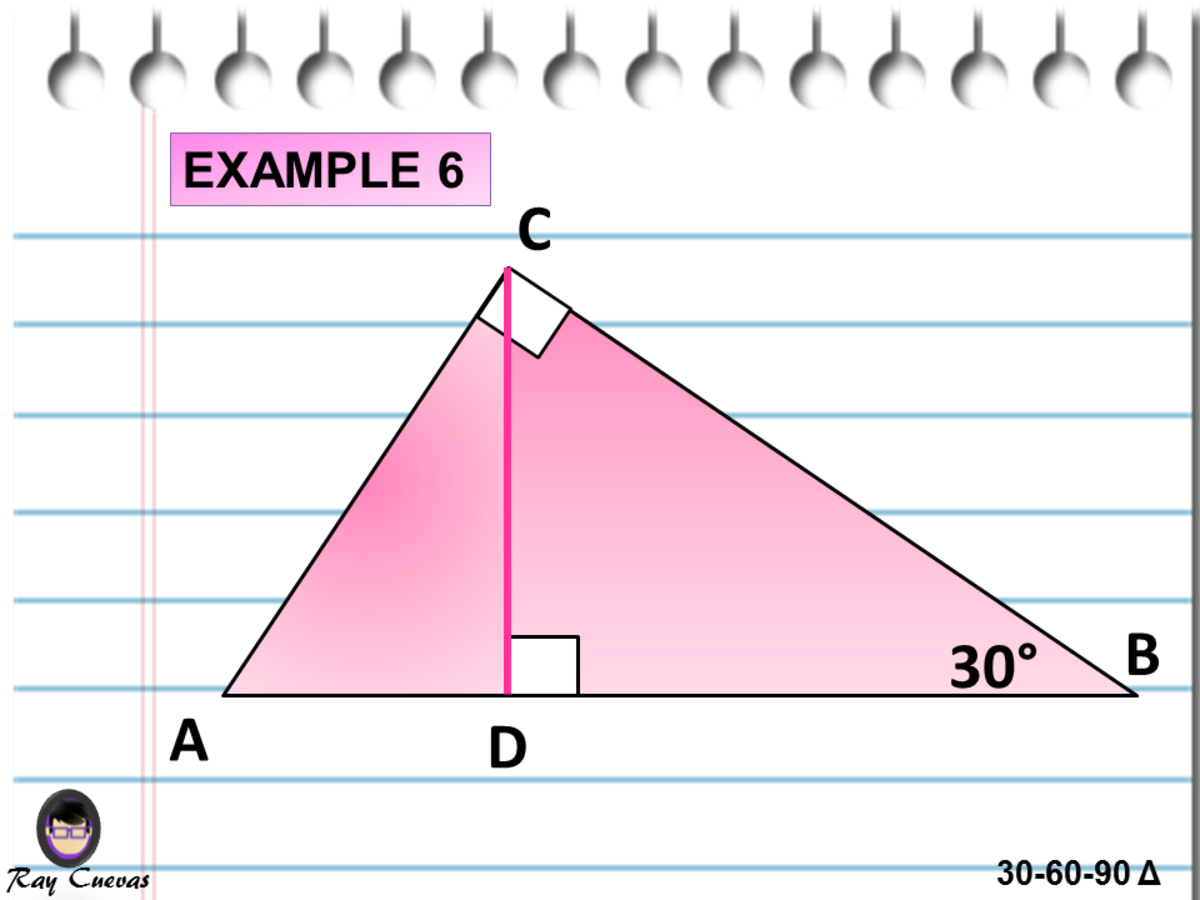



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



The Easy Guide To The 30 60 90 Triangle




How To Use The Special Right Triangle 30 60 90 Studypug
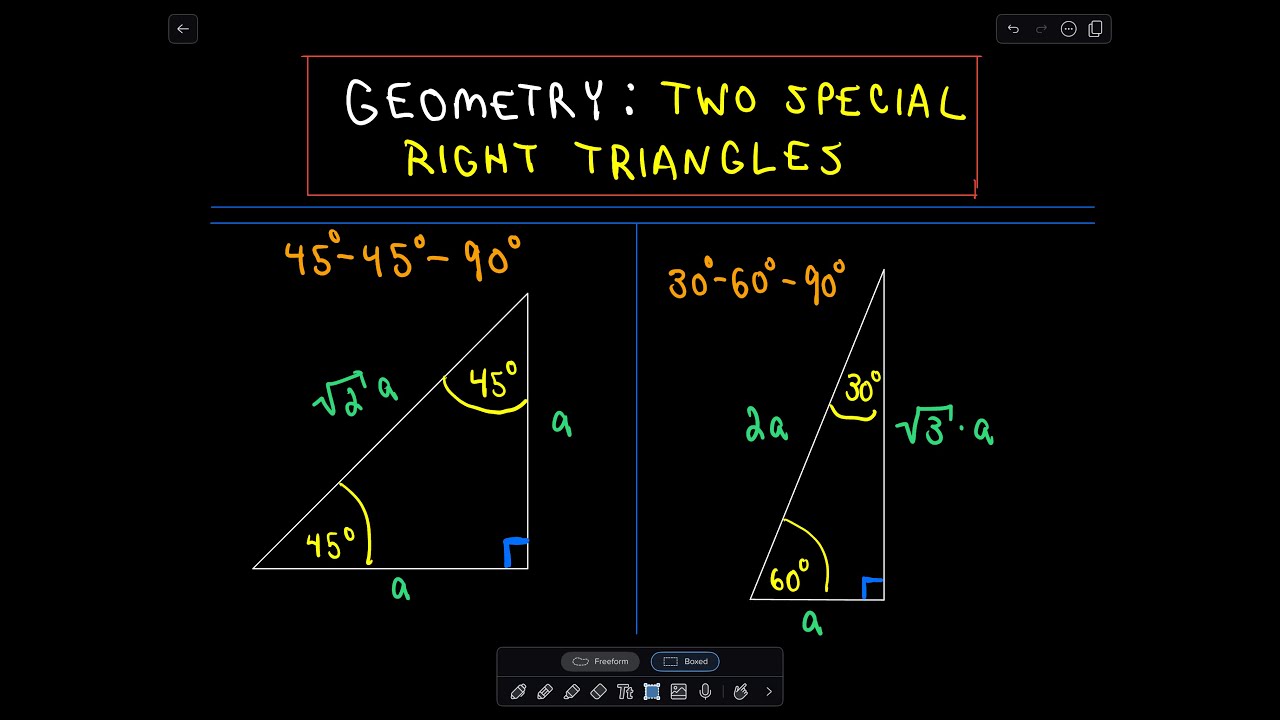



Special Right Triangles In Geometry 45 45 90 And 30 60 90 Youtube




A Quick Guide To The 30 60 90 Degree Triangle Dummies



Special Right Triangle 30 60 45 45 37 53 Elearning
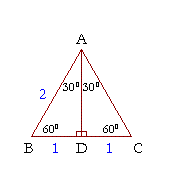



30 60 90 Right Triangle Side Ratios Expii
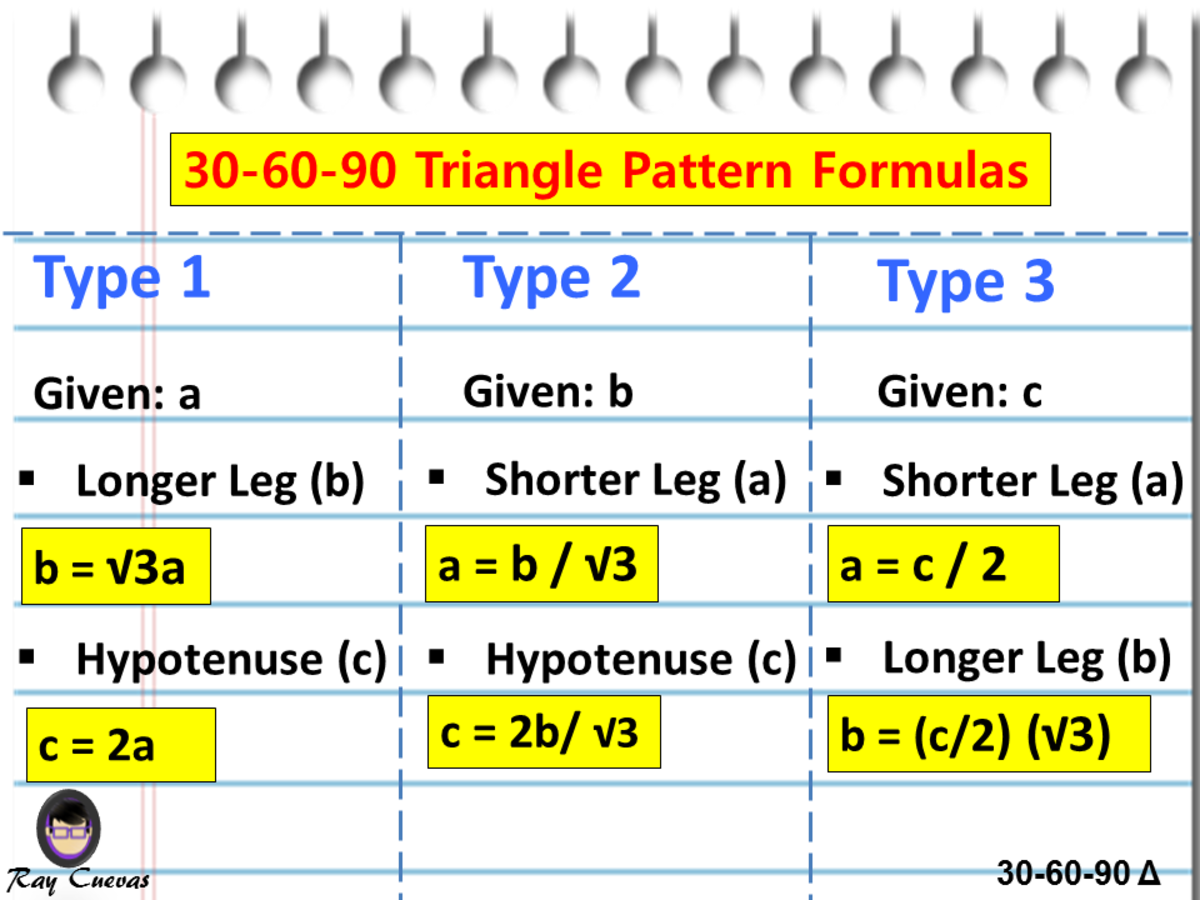



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Formulas Rules And Sides Science Trends
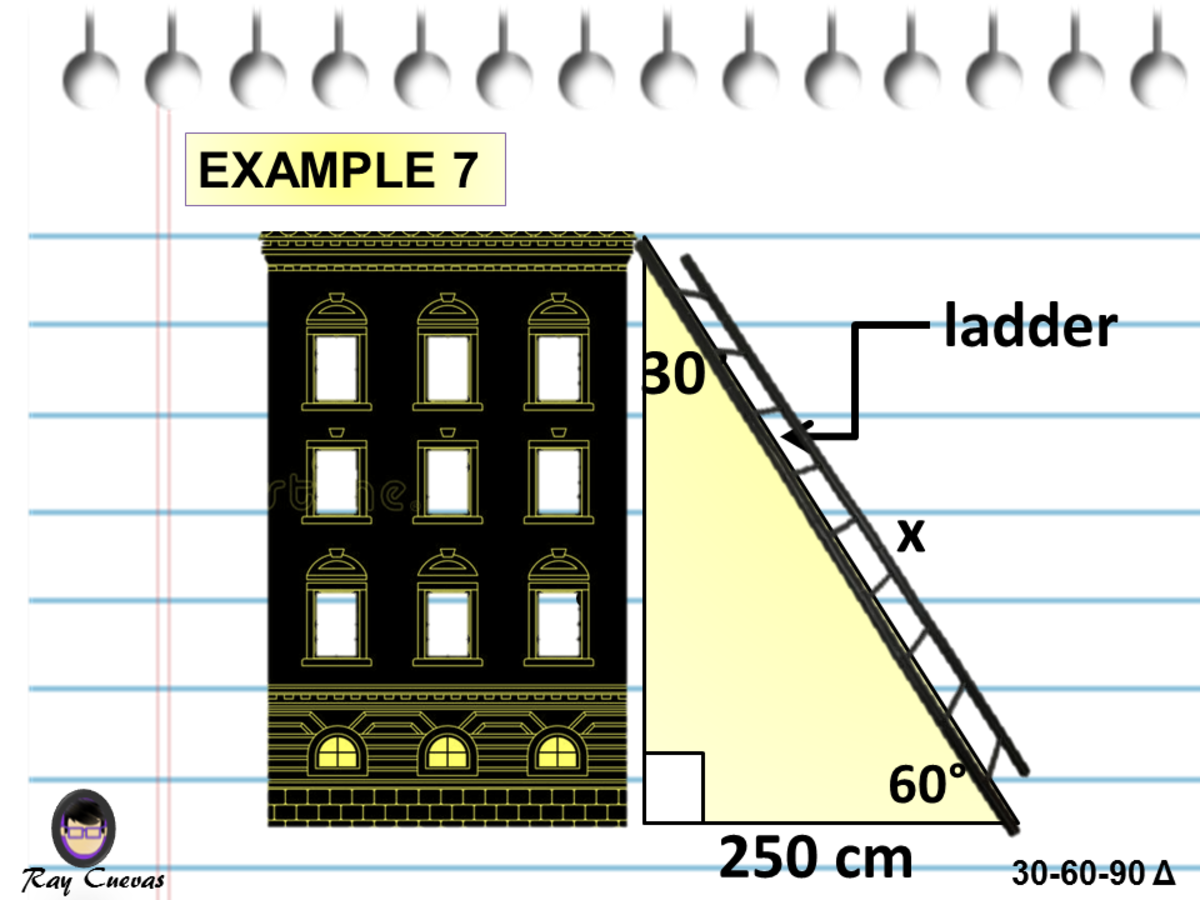



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Explanation Examples
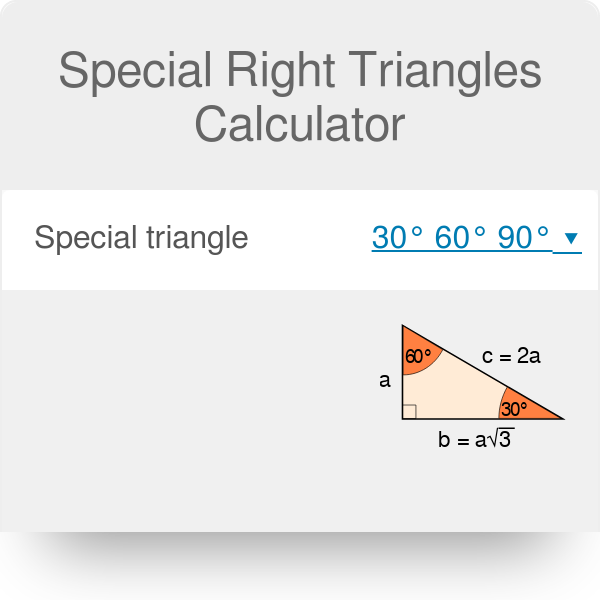



Special Right Triangles Calculator Formula Rules




30 60 90 Triangle Theorem Ratio Formula Video
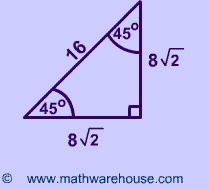



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems




5 30 60 90 Triangles Geometry15a
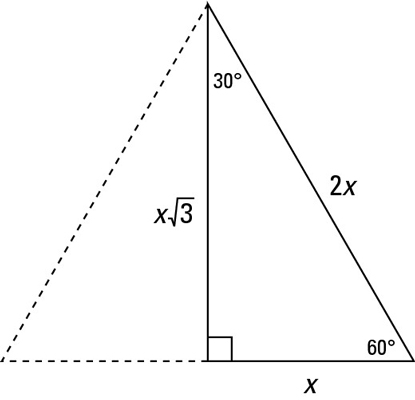



Identifying The 30 60 90 Degree Triangle Dummies



The Easy Guide To The 30 60 90 Triangle



Right Triangles Gmat Free




How To Find The Sides Of A 30 60 90 Right Triangle Math Wonderhowto




30 60 90 Triangle Theorem Proof Don T Memorise Youtube




Special Right Triangles Video Lessons Examples And Solutions
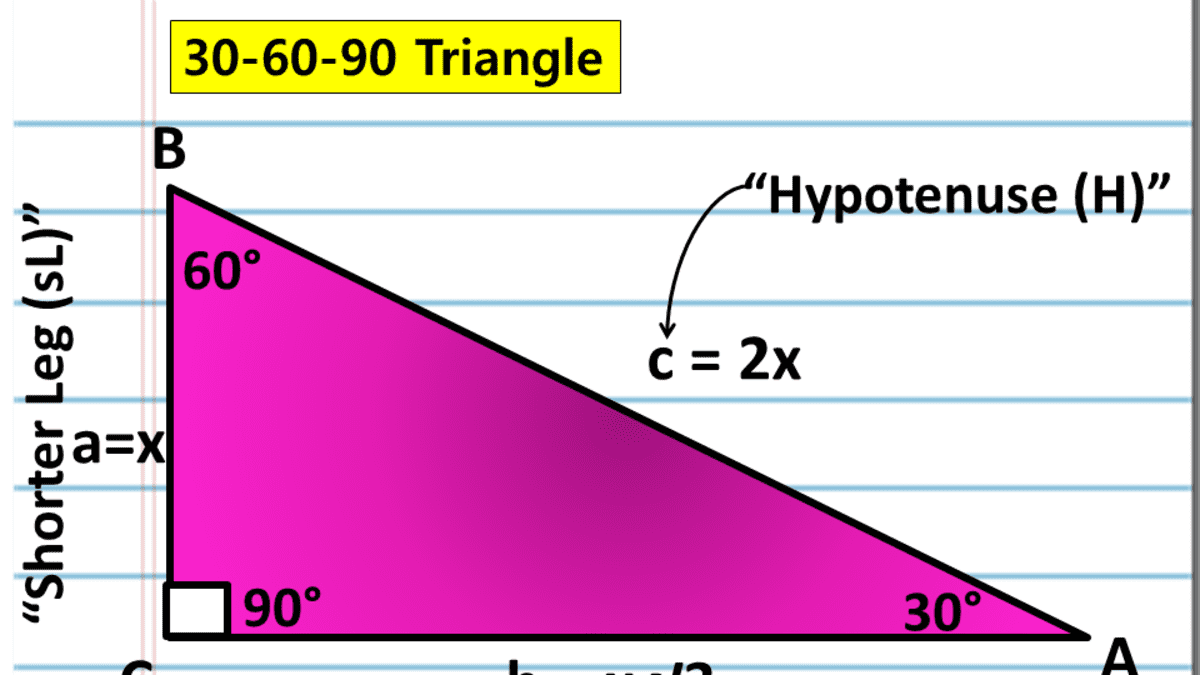



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Special Right Triangle Calculator General Knowledge Book Right Triangle Electrical Engineering Books
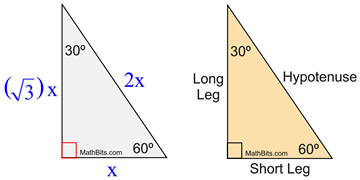



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math
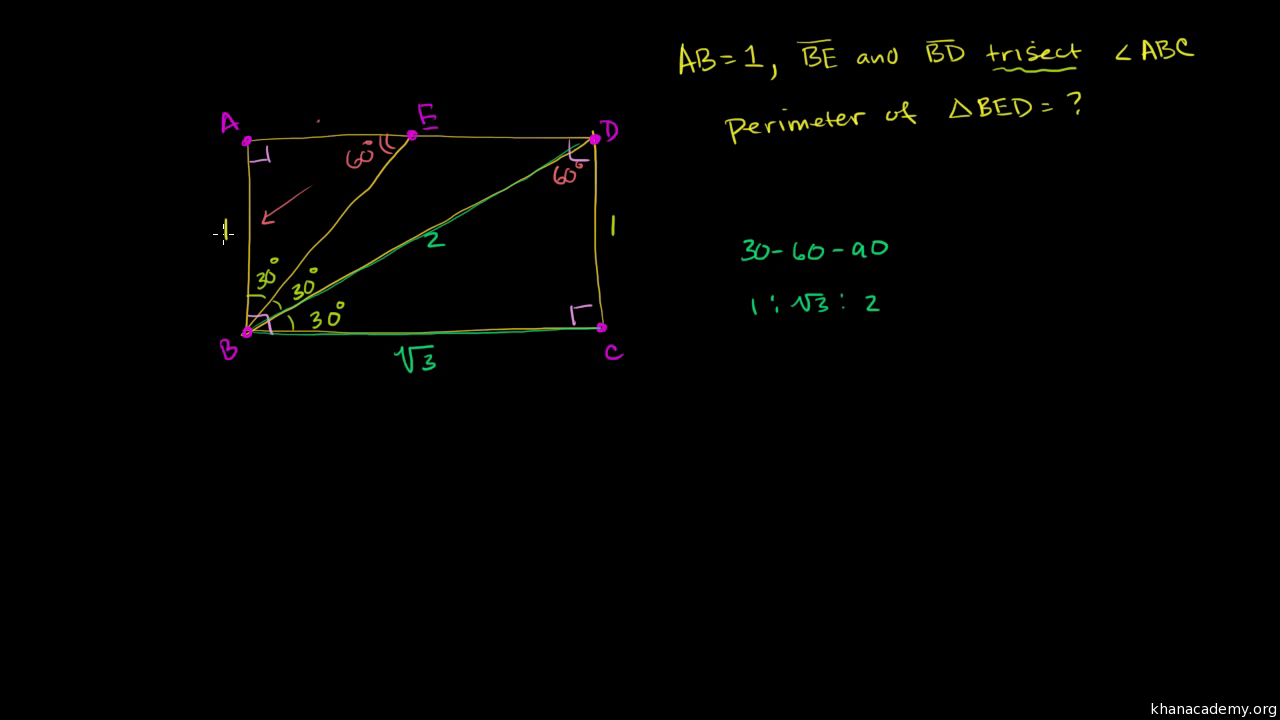



30 60 90 Triangle Example Problem Video Khan Academy




30 60 90 Triangle Explanation Examples
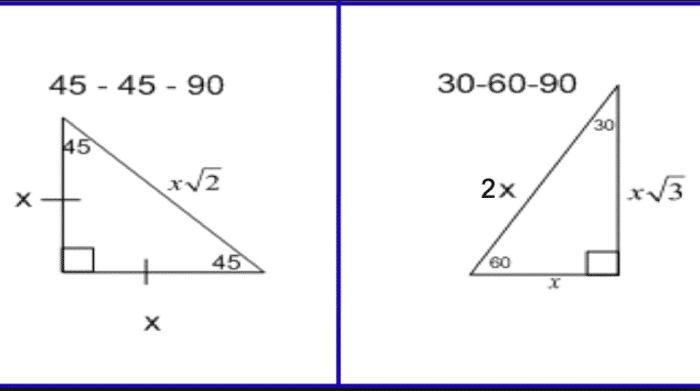



Special Right Triangles Complete Reference Guide The Education




30 60 90 Right Triangles Free Math Help




A Quick Guide To The 30 60 90 Degree Triangle Dummies




The Complete Guide To The 30 60 90 Triangle




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Theorem Ratio Formula Video




Special Right Triangle Wikipedia
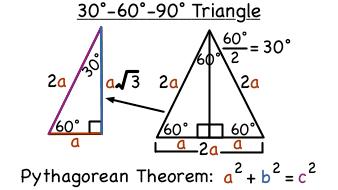



What Is A 30 60 90 Degree Triangle Virtual Nerd




Geometry 8 4 Special Right Triangles This Is




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




Velocity




The 30 60 90 Triangle Topics In Trigonometry




The Complete Guide To The 30 60 90 Triangle




Special Right Triangles Fully Explained W 19 Examples




30 60 90 Right Triangles Solutions Examples Videos




30 60 90 Math Methods Studying Math Physics And Mathematics




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



45 45 90 And 30 60 90 Triangles Zona Land Education




30 60 90 Triangle Theorem Ratio Formula Video



1




30 60 90 Triangle Calculator Formula Rules




How To Work With 30 60 90 Degree Triangles Education Is Around




30 60 90 Special Right Triangle Calculator Inch Calculator



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangles



30 60 90 Triangle Rules
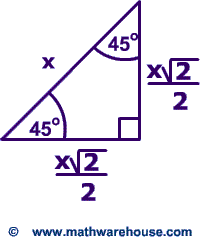



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems




Right Triangles Interactive Notebook Pages Mrs E Teaches Math



1




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangles Special Right Triangle Trigonometry Youtube



The Easy Guide To The 30 60 90 Triangle



30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Theorem Ratio Formula Video
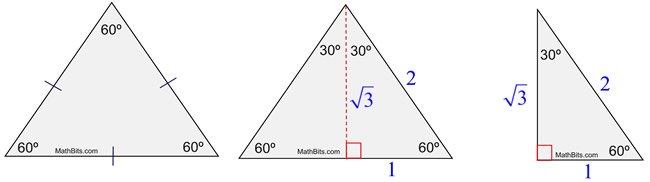



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math



Solve A 30 60 90 Triangle With Gradea




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube




30 60 90 Triangle Explanation Examples




Special Right Triangles Review Article Khan Academy




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



Special Right Triangles Geometry
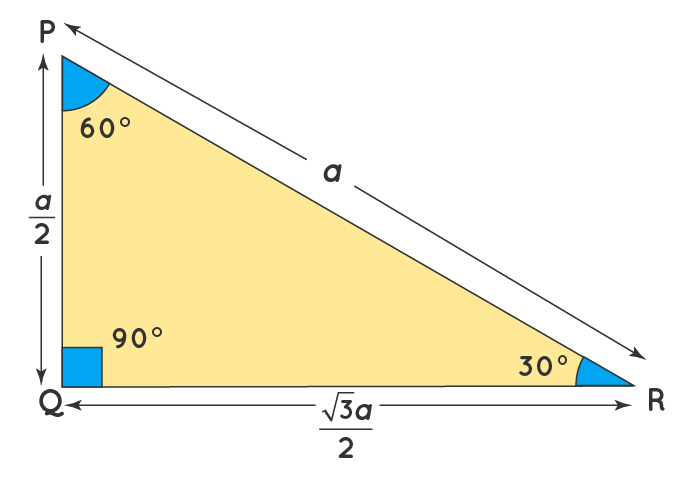



30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Definition Theorem Formula Examples



0 件のコメント:
コメントを投稿